Question

4. Rhombus QRST has diagonals intersecting at W. Point U is located on side QR and point V on diagonal RT

such that UV is perpendicular to QR.

Prove: QW•UR =WT•UV
​

Answer 1

Given:

In Rhombus QRST, diagonals QS and RT intersect at W and U∈QR and point V∈RT such that UV⊥QR. (shown in below diagram)

To prove: QW•UR =WT•UV

Proof:

In a rhombus diagonals bisect perpendicularly,

Thus, in QRST

QW≅WS, WR ≅ WT and m∠QWR=m∠QWT=m∠RWS=m∠TWS=90°.

In triangles QWR and UVR,

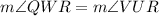`m\angle QWR=m\angle VUR` (Right angles)

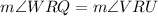`m\angle WRQ=m\angle VRU` (Common angles)

By AA similarity postulate,

`\triangle QWR\sim \triangle VUR`

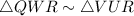
The corresponding sides in similar triangles are in same proportion,

`\implies (QW)/(VU)=(WR)/(UR)`

`QW* UR=WR* VU`

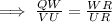
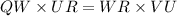
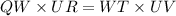`QW* UR=WT* UV` (∵ WR ≅ WT )

Hence, proved.