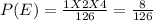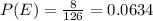Question

Suppose we have an urn containing 9 marbles. Two are red, three are green, and four are blue. We randomly select 5 marbles from the urn, with replacement. What is the probability of selecting 3 green marbles, 1 red marble, and 1 blue marbles?

Answer 1

probability of selecting 3 green marbles, 1 red marble, and 1 blue marbles

`P(E) =(8)/(126) = 0.0634`

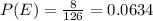
Explanation:

Given data urn containing '9' marbles

given red marbles = 2

green marbles =3

blue marbles = 4

Five marbles can be selected at a time from '9' marbles in
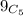`9_{C_(5) }` ways

by using formula
`n_{C_(r) }=(n!)/((n-r)!r!)`

`9_{C_(5) }=(9!)/((9-5)!5!) = (9X8X7X6X5!)/(4!5!)`

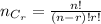
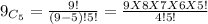
After simplification , we get
`9_{C_(5) } = 126`

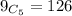
total number of ways n(S) = 126

The probability of selecting '3' green marbles ,one red marble and one blue marble with replacement.

let ' E' be the event of selecting '3' green marbles ,one red marble and one blue marble with replacement.

n(E) =
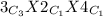`3_{C_(3) } X2_{C_(1) }X 4_{C_(1) }` ways

The required probability
`P(E) = (n(E))/(n(S))`

`p(E) = \frac{3_{C_(3) } X2_{C_(1) }X 4_{C_(1) }}{9_{C_(5) } }`

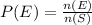
on simplification , we get

`P(E) = (1X2X4)/(126) =(8)/(126)`

`P(E) =(8)/(126) = 0.0634`