Question

Right △EFG has its right angle at G, EF=8 , and FG=6 . What is the value of the trigonometric ratio of an angle of the triangle? Drag a value to each box to match the trigonometric ratio with its value.

Answer 1

e are required to find;

Tan G

cos E

sec G

The answers tot the question are;

Tan E = 3/√7

Cos E = √7/4

Sec F = 4/3.

Explanation:

To solve the question, we note that the triangle has the following angles and sides

FG = 6 EF =8 and angle G = 90°

The third side of the right angled triangle is therefore GE

The side EF is the hypotenuse side as it is opposite the right angle (angle 90) in the triangle

Therefore the length of the side GE is given by

GE =
`√(EF^2-FG^2)` =
`√(8^2-6^2)` = √28 = 2√7

Therefore the trigonometric ratios are as follows

Tan E

Tan E is given by Tan E =
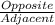`(Opposite)/(Adjacent )` = FG/GE = 3/√7

cos E

Cos E is given by Cos E =
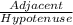`(Adjacent )/(Hypotenuse)` = GE/EF = 1√7/4

sec F

Sec F = 1/(cos F) = 1÷
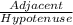`(Adjacent )/(Hypotenuse)` = EF/FG = 8/6 =4/3.