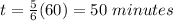Answer:
50 minutes
Explanation:
we know that
The speed is equal to divide the distance by the time
Let
s ----> the speed in miles per hour
d ---> the distance in miles
t ---> the time in hours
so
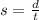
step 1
Upstream
Find the time
we know that
The speed upstream is equal to the average speed still water minus the average speed of the river
so
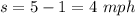
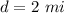
substitute
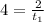
solve for t_1

simplify

step 2
Downstream
Find the time
we know that
The speed downstream is equal to the average speed still water plus the average speed of the river
so
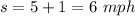
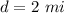
substitute
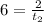
solve for t_2
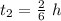
simplify
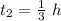
step 3
Find the total time
Adds t_1 and t_2
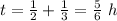
Convert to minutes
Multiply by 60