Answer:
(a). The work done by the applied force is 328.89 J.
(b). The work done by the normal force is zero.
(c). The work done by the force of gravity is zero.
(d). The work done by the force of friction is 184.5 J.
Step-by-step explanation:
Given that,
Force = 70 N
Mass of block = 15 kg
Angle = 20°
Displaced = 5.00 m
Coefficient of kinetic friction = 0.300
(a). We need to calculate the work done by the applied force
Using formula of work done
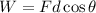
Put the value into the formula
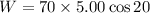
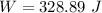
(b). We need to calculate the work done by the normal force
The normal force is perpendicular to the displacement of the motion,
So it does not work.
(c). We need to calculate the work done by the force of gravity
The gravitational force is perpendicular to the displacement,
Or the displacement in the vertical direction is zero.so the work done is zero.
(d). We need to calculate the normal force
Using balance equation
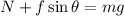
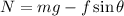
Put the value into the formula
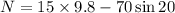
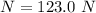
We need to calculate the force of friction
Using formula of friction

Put the value into the formula
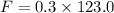
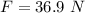
We need to calculate the work done by the force of friction
Using formula of work done
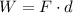
Put the value into the formula


Hence, (a). The work done by the applied force is 328.89 J.
(b). The work done by the normal force is zero.
(c). The work done by the force of gravity is zero.
(d). The work done by the force of friction is 184.5 J.