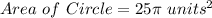Question

A circle has a sector with area \dfrac{45}{4}\pi 4 45 ​ πstart fraction, 45, divided by, 4, end fraction, pi and central angle of \purple{\dfrac{9}{10}\pi} 10 9 ​ πstart color #9d38bd, start fraction, 9, divided by, 10, end fraction, pi, end color #9d38bd radians . What is the area of the circle?

Answer 1

10 pi cm square

Explanation:

khan academy

Answer 2

Therefore,

`Area\ of\ Circle = 25\pi \ units^(2)`

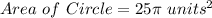
Explanation:

Given:

`Area\ of\ sector = (45)/(4)\pi`

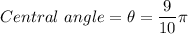`Central\ angle =\theta = (9)/(10)\pi` ( in Radians)

To Find:

Area of Circle = ?

Solution:

If "θ" is measured in radians then area of sector is given by,

`Area\ of\ sector = (1)/(2)* r^(2)\theta`

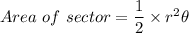
Where,

θ = Central angle in radians

r =radius of a circle

Substituting the values we get

`(45)/(4)\pi= (1)/(2)* r^(2)* (9)/(10)\pi`

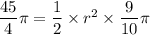
On solving we get

`r^(2)=25\\\\Square\ Rooting\\\\r = √(25)=5\ units`

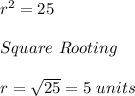
Now, Area of Circle is given by,

`Area\ of\ Circle = \pi r^(2)`

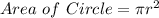
Substituting the values we get

`Area\ of\ Circle = 25\pi \ units^(2)`

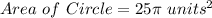
Therefore,

`Area\ of\ Circle = 25\pi \ units^(2)`