Answer:
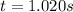
Explanation:
Given Equation:
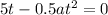
Actually the given equation is the 2nd equation of motion
i.e.
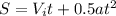
where
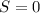 because the astronaut jumps on the earth
because the astronaut jumps on the earth
and initial velocity
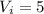
to find time
 , put the given value of
, put the given value of
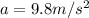 in the given equation, we get
in the given equation, we get
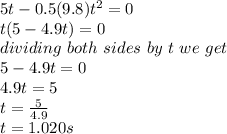
it will take
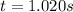 to reach the ground if he jumps on the Earth
to reach the ground if he jumps on the Earth