Question

550 people use a public swimming pool the prices are 1.75$ for children and 2.25$ for adults the receipts for admission totaled is 1153.00$ How many children were at the pool

Answer 1

There were 169 children at the pool.

Explanation:

Given:

Total number of people = 550

Price per child = $1.75

Price per adult = $2.25

Total cost of the admission receipts = $1153.00

Let the number of children be 'x' and number of adults be 'y'.

As per question:

Total number of people is equal to total children and total adults. So,

`x+y=550-----------(1)`

Total cost of admission is equal to the sum of cost of total children and total adults. So,

`1.75x+2.25y=1153-----------(2)`

Multiplying equation (1) by 1.75 and subtracting the result equation from equation (2). This gives,

`1.75x+1.75y=962.5\\\\\\1.75x+2.25y=1153\\1.75x+1.75y=962.5\\(-)\\-------------\\0.5y=190.5\\\\y=(190.5)/(0.5)=381`

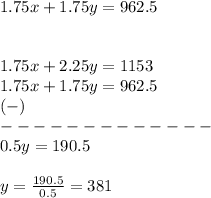
So, there were 381 adults at the pool. Now, the number of children is equal to:

`x=550-y=550-381=169`

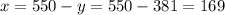
Therefore, there were 169 children at the pool.