Answer:
The dimension of the patio are approximately 12.82 ft × 14.82 ft.
Explanation:
Given:
Length of the patio =
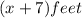
Width of the patio =

Area of the patio =
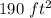
We need to find the dimensions of the patio.
Solution:
Now we know that;
Area of the rectangle is equal to length times width.
framing in equation form we get;
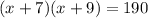
Applying distributive property we get;
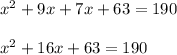
Now adding 1 on both side we get;

Now taking square root on both side we get;

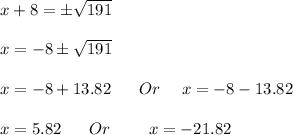
Now we got two values of x one positive and 1 negative now we know that dimension of the patio cannot be negative; so we will discard negative value and consider positive value.
Length of the patio =

Width of the patio =

Hence the dimension of the patio are approximately 12.82 ft × 14.82 ft.