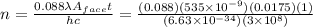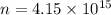Question

Suppose that you have a 10 Watt green LED lamp, that emits light at a wavelength of 535 nm uniformly in all directions. 1) Suppose that you look at the lamp from a distance of 3 meters. If your face has an area of 175 cm2 facing the LED, how many photons from the lamp hit your face each second?

Answer 1

Each second approximately
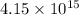`4.15*10^(15)` photons hit the face

Step-by-step explanation:

Emmited intensity of electromagentic waves is defined as:

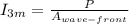`I_(3m)=(P)/(A_(wave-front))` (1)

with P the power and A_{wave-front} the surface of the sphere that defines the wave front at a given radial distance (r) from the source, this is:

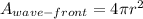`A_(wave-front)=4\pi r^2` (2)

Using (2) on (1):

`I_(3m)=(P)/(4\pi d^2)=(10)/(4\pi 3^2)`

`I_(3m)=0.088 (W)/(m^(2))`

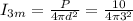
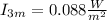
That is the intensity of ligth at 3 meters from the source so that it's the intensity the face absorbs so again using equation (1) but now for absorbed intensity:

`I_(abs)=0.088 =(P)/(A_(face))` (3)

Power is the energy over a perioid of time this is:

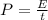`P=(E)/(t)` (4)

But energy of photons is:

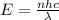`E= (nhc)/(\lambda)` (5)

with n the number of photons, h Planck's constant,c velocity odf ligth and
`\lambda` the wavelength

Using (5) on (4) and (4) on (3):

`0.088 =(nhc)/(\lambda A_(face) t)`

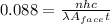
Solving for n

`n=(0.088 \lambda A_(face) t)/(hc)=((0.088) (535*10^(-9)) (0.0175)(1))/((6.63*10^(-34)) (3*10^(8)))`

`n=4.15*10^(15)`