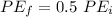Answer:
The relationship between the initial stored energy
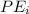 and the stored energy after the dielectric is inserted
and the stored energy after the dielectric is inserted
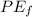 is:
is:
c)
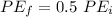
Step-by-step explanation:
A parallel plate capacitor with
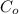 that is connected to a voltage source
that is connected to a voltage source
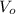 holds a charge of
holds a charge of
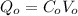 . Then we disconnect the voltage source and keep the charge
. Then we disconnect the voltage source and keep the charge
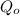 constant . If we insert a dielectric of
constant . If we insert a dielectric of
 between the plates while we keep the charge constant, we found that the potential decreases as:
between the plates while we keep the charge constant, we found that the potential decreases as:
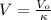
The capacitance is modified as:
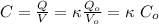
The stored energy without the dielectric is
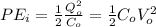
The stored energy after the dielectric is inserted is:

If we replace in the above equation the values of V and C we get that
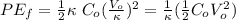
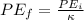
Finally