Question

A telephone pole is installed so that 25 feet of the pole are above ground level. A stabilizing cable is anchored to the ground 44 inches from the base of the pole. The other end of the cable is attached to the pole at a point 20 feet above ground level. To the nearest inch, how many inches long is the stabilizing cable?

Answer 1

`\huge\boxed{244\ \text{inches}}`

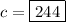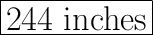
This problem can be solved using the Pythagorean Theorem.

Note: the height of the telephone pole is unnecessary information.

Convert the measurement in feet to inches.

`20*12=240`

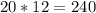
The length from the base of the pole to the anchor point on the ground is
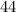`44` inches. The distance from the base of the pole to the anchor point on the pole is
`240` inches.

These are the two legs of a right triangle. The length of the stabilizing cable is the hypotenuse of the right triangle.

The Pythagorean Theorem is:

`a^2+b^2=c^2`

In this formula,
`a` and
`b` are the legs and
`c` is the hypotenuse.

Plug in the known values.

`44^2+240^2=c^2`

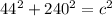
Swap the sides of the equation.

`c^2=44^2+240^2`

Evaluate the powers.

`c^2=1936+57600`

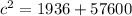
Simplify using addition.

`c^2=59536`

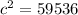
Take the square root of both sides.

`c=\pm 244`

Separate the solutions.

`c=244\\c=-244`

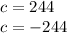
Length and distance cannot be negative, so remove the negative solution.

`c=\boxed{244}`