Question

Suppose you have 100 ft of string to rope off a rectangular section for a bake sale at a school Fair. The function A=x^2+50x gives the area of the section in square feet, where x is the width in feet. What width gives you the maximum area you can rope off? What is the maximum area? What is the range of the function?

Answer 1

Therefore the width is 25 feet for getting maximum area.

The maximum area of the rectangle is 625 square feet.

Therefore the range is 0≤A≤625.

Explanation:

Given function is

A = - x²+50x

We know that ,

If y = ax²+bx+c

For the maximum
`x=-(b)/(2a)`

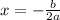
Here a = -1 , b= 50 and c=0

Therefore the width
`x= -(50)/(2.(-1)) = 25`

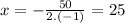
Therefore the width is 25 feet for getting maximum area.

The maximum area =[ -(25)²+50.25] square feet

= 625 square feet

The area can not be negative and maximum area is 625 square feet.

Therefore the range is 0≤A≤625.