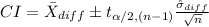Question

A salesman for a shoe company claimed runners would run faster races if they wore the company's brand of running shoe. A track coach wanted to see how much faster his runners would run, if they wore the company's shoes. He randomly selected 8 runners and had each of them run the 100-yard dash, twice. They wore their usual shoes to run the race on one day, and they wore the company's shoe to run the race on another day. Their times for both races were recorded, and the coach randomly selected the day each runner would wear the company's brand of shoe. Which confidence interval would be most appropriate for this study?a. ne sample z-confidence intervalb. One sample t-confidence intervalc. Paired-samples t-confidence intervald. Two sample t-confidence interval

Answer 1

Correct option: (c) Paired samples t confidence interval.

Explanation:

A paired data is collected from an experiment that is conducted twice; once before applying a treatment and second time after the treatment has been applied.

For example, scores of students before the coaching classes and after the coaching classes.

In this case a paired data is collected.

The runners were asked to run 100-yard wearing their usual shoes one day and do same thing the next day wearing the company's shoes.

The two data collected from both the days is a paired data.

To determine whether the salesman's claim that the runners would run faster races if they wore the company's brand of running shoe is correct or not a confidence interval can be constructed for the paired the data.

If the true mean difference is contained in the interval then the salesman's claim can be considered true otherwise false.

To construct this confidence interval use a paired sample t confidence interval.

Because the population standard deviations are not known.

The (1 - α)% confidence interval for the paired difference is:

`CI=\bar X_(diff)\pm t_(\alpha/2, (n-1)) (\hat \sigma_(diff))/(√(n))`