Question

The 630-nm light from a helium-neon laser irradiates a grating. The light then falls on a screen where the first bright spot is separated from the central maximum by 0.61 m. Light of another wavelength produces its first bright spot 0.45 m from its central maximum. Determine the second wavelength.

Answer 1

464.8 nm

Step-by-step explanation:

The second wavelength of light can be calculated using the next equation:

`\lambda = (x*d)/(L)`

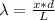
Where:

λ : is the wavelength of light

x: is the distance from the central maximum

d: is the distance between the spots

L: is the lenght from the screen to the bright spot

For the first wavelength of light we have:

`\lambda_(1) = (x_(1)*d)/(L)`

`630 \cdot 10^(-9) m = (0.61 m*d)/(L)`

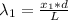
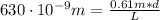
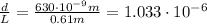`(d)/(L) = (630 \cdot 10^(-9) m)/(0.61 m) = 1.033 \cdot 10^(-6)` (1)

For the second wavelength of light we have:

`\lambda_(2) = (x_(2)*d)/(L)`

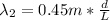`\lambda_(2) = 0.45 m*(d)/(L)` (2)

By entering equation (1) into equation (2) we have:

`\lambda_(2) = 0.45 m* 1.033 \cdot 10^(-6) = 4.648 \cdot 10^(-7) m = 464.8 nm`

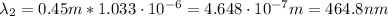
Therefore, the second wavelength is 464.8 nm

I hope it helps you!