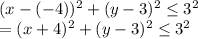Answer:
The correct answer is:
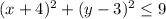
Explanation:
The airport is located at the point (-4 , 3). Thus we can consider the center of the circle to be this particular point.
Since the noise can be heard till 3 miles away, this implies we can consider the radius of the circle to be 3.
We all know the general equation of circle with center at (
 ,
,
 ) with radius r is given by:
) with radius r is given by:
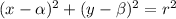
Here the value of
 is (-4) ; value of
is (-4) ; value of
 is 3 ; and value of r is 3.
is 3 ; and value of r is 3.
Now since the noise of landing and taking off of the planes would be within the circle, hence we use less than equal to (
 ) sign instead of equal to sign.
) sign instead of equal to sign.
Thus the general equation of noise of the planes can be given by the inequality