Question

A survey finds customers are charged incorrectly for 44 out of every 10 items. Suppose a customer purchases 1414 items. Find the probability that the customer is charged incorrectlyis charged incorrectly on at mostmost 22 items.

Answer 1

The probability that the customer is charged incorrectly on at most 2 items is 3.979 × 10⁻².

Explanation:

To solve the question, we note that we proceed with the binomial distribution formula as follows

Number of times the customer is incorrectly charged out of ever 10 items = 4

Therefore, the probability that the customer is incorrectly charged is 4/10 = 0.4

That is p(incorrect) = 0.4

Then the probability that the customer is charged incorrectly on at most 2 items is

P(x≤2) = P(x=0) + P(x=1) + P(x=2)

= ₙC
`_r` ×
`p^r`×
`q^((n-r))` =

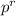P(x=0) = ₁₄C₀ ×0.4⁰× 0.6¹⁴ = 7.836 × 10⁻⁴

P(x=1) = ₁₄C₁ ×0.4¹× 0.6¹³ = 7.314 × 10⁻³

P(x=2) = ₁₄C₂ ×0.4²× 0.6¹² = 3.169 × 10⁻²

∴ P(x≤2) = 7.836 × 10⁻⁴ + 7.314 × 10⁻³ + 3.169 × 10⁻² = 3.979 × 10⁻²

P(x≤2) = 3.979 × 10⁻².