A. Convert 5x^2 + 55x + 140 from standard to vertex form b. Describe the transformation.

Question

asked Jul 28, 2023 86.7k views

2 Answers

Jeremy Smyth · Answer 1 · 2023-07-30T15:46:57+0000

Answer:

See below.

Explanation:

5x^2 + 55x + 140 ---> required

Coefficients a=5, b=55, c=140 yield

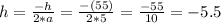
h=(-h)/(2*a) =(-(55))/(2*5) =(-55)/(10) =-5.5

Thus, the x-coordinate of the vertex is
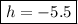
$\boxed{h = -5.5 }$

Plugging x=-5.5 into the given equation yields:

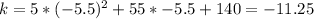
k=5*(-5.5)^(2) +55*-5.5+140=-11.25

Thus, the y-coordinate of the vertex is
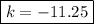
$\boxed{k = -11.25 }$

Altogether, the vertex of the given parabola is

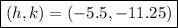
$\boxed{ (h,k)=(-5.5,-11.25) }$

Plugging (h,k)=(−5.5,−11.25) into the vertex formula

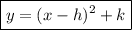
$\boxed{ y=(x-h)^2+k }$

yields the vertex form of the parabola

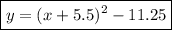
$\boxed{ y=(x+5.5)^2-11.25 }$

To find the vertex of a parabola in standard form, first, convert it to the vertex form y=a(x−h)2+k y = a ( x − h ) 2 + k .