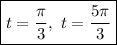Answer:
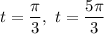
Explanation:
Trigonometric Equations
The given equation is
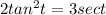
To solve the equation we must recall that

Substituting into the given equation
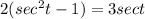
Operating and rearranging
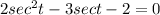
This is a second-degree equation in terms of sect. Factoring
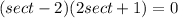
This produces two solutions
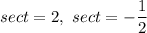
Recalling
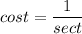
The solutions are also expressed as

since the magnitude of the cosine cannot be greater than 1, the only acceptable solution is
\displaystyle cost=\frac{1}{2}
Which has two possible angles in the interval [0,2\pi]