Answer:
The magnetic field strength is 0.679 T.
Step-by-step explanation:
Given:
Number of turns (N) = 250
Current in the coil (I) = 3.9 A
Diameter of the coil (d) = 6.2 cm =0.062 m [1 cm = 0.01 m]
Maximum torque is,
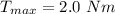
First, let us calculate the area of the coil.
Area is given by the formula:
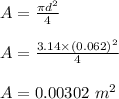
Now, the torque acting on the circular coil is given by the formula:
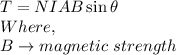
Now, torque is maximum when the angle
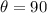 ° or
° or
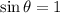
Therefore, the maximum torque is given as:
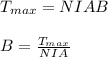
Now, plug in the given values and solve for 'B'. This gives,
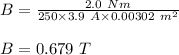
Therefore, the magnetic field strength is 0.679 T.