Question

A triangular bandana has an area of 34 square inches. The height of the triangle is 8 1/2 inches. Enter and solve an equation to find the length of the base of the triangle. Use b to represent the length of the base.

Answer 1

8 inches

Explanation:

Use the formula for area of a triangle:

A = bh/2

"A" for area

"b" for base

"h" for height

What we know:

A = 34in²

h = 8 1/2 in

Substitute the known values into the formula

A = bh/2

(34in²) = b(8 1/2 in)/2

Isolate "b" to solve for the length of the base

(34in²) * 2 = b(8 1/2 in)/2 * 2 Multiply both sides by 2.

(68in²) = b(8 1/2 in)

(68in²)/(8 1/2 in) = b(8 1/2 in)/(8 1/2 in) Divide both sides by (8 2/1 in)

(68in²)/(8 1/2 in) = b Simplify and move variable to left

b = (68in²)/(8 1/2 in)

How to divide a mixed fraction:

`b = (68in^(2))/(8(1)/(2) in)`

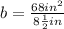
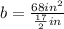`b = (68in^(2))/((17)/(2) in)` Convert to improper fraction

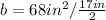`b = 68in^(2) / (17in)/(2)` Reformat division

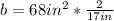`b = 68in^(2) * (2)/(17in)` Flip the second fraction

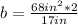`b = (68in^(2) * 2)/(17in)` Combine into numerator

`b = 8in` Length of base

Therefore the base is 8 inches.