Question

The ratio of the lift force L to the drag force D for the simple airfoil is L/D = 10. If the lift force on a short section of the airfoil is 64 lb, compute the magnitude of the resultant force R and the angle θ which it makes with the horizontal.

Answer 1

`R=64.32\ lb\\\\\theta=84.3\°`

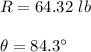
Step-by-step explanation:

Given:

Ratio of lift force to drag force is,
`(L)/(D)=10`

Lift force on a short section is,
`L=64\ lb`

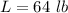
Magnitude of resultant,
`R= ?`

The angle of 'R' with the horizontal is,
`\theta=?`

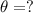
We know that, lift force and drag are at right angles to each other. So, the resultant can be computed using Pythagoras theorem.

For calculating 'R', we first compute drag force 'D'.

As per question:

`(L)/(D)=10\\\\D=(L)/(10)=(64\ lb)/(10)=6.4\ lb`

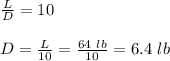
Now, the magnitude of resultant 'R' is given as:

`R=√(L^2+D^2)`

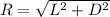
Plug in the given values and solve for 'R'. This gives,

`R=√(64^2+6.4^2)\\\\R=√(4096+40.96)\\\\R=√(4136.96)=64.32\ lb`

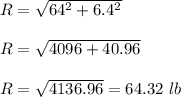
Therefore, the magnitude of the resultant force 'R' is 64.32 lb.

Now, the angle
`\theta` is given as the arctan of the ratio of the lift and drag force.

Therefore,

`\theta=\tan^(-1)(L/D)\\\\\theta=\tan^(-1)(10)\\\\\theta=84.3\°`

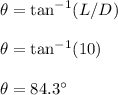
Therefore, the angle made with the horizontal is 84.3°.