Question

An inverted pyramid is being filled with water at a constant rate of 45 cubic centimeters per second. The pyramid, at the top, has the shape of a square with sides of length 6 cm, and the height is 13 cm. Find the rate at which the water level is rising when the water level is 4 cm.

Answer 1

13.20 cm/s is the rate at which the water level is rising when the water level is 4 cm.

Step-by-step explanation:

Length of the base = l

Width of the base = w

Height of the pyramid = h

Volume of the pyramid =
`V=(1)/(3)lwh`

We have:

Rate at which water is filled in cube =
`(dV)/(dt)= 45 cm^3/s`

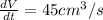
Square based pyramid:

l = 6 cm, w = 6 cm, h = 13 cm

Volume of the square based pyramid = V

`V=(1)/(3)* l^2* h`

`(l)/(h)=(6)/(13)`

`l=(6h)/(13)`

`V=(1)/(3)* ((6h)/(13))^2* h`

`V=(12)/(169)h^3`

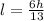
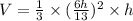
Differentiating V with respect to dt:

`(dV)/(dt)=(d((12)/(169)h^3))/(dt)`

`(dV)/(dt)=3* (12)/(169)h^2* (dh)/(dt)`

`45 cm^3/s=3* (12)/(169)h^2* (dh)/(dt)`

`(dh)/(dt)=(45 cm^3/s* 169)/(3* 12* h^2)`

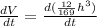
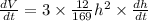
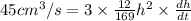
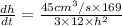
Putting, h = 4 cm

`(dh)/(dt)=(45 cm^3/s* 169)/(3* 12* (4 cm)^2)`

`=13.20 cm/s`

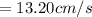
13.20 cm/s is the rate at which the water level is rising when the water level is 4 cm.