Question

An internet search engine looks for a certain keyword in a sequence of independent web sites. It is believed that 20% of the sites contain this keyword. (a) Compute the probability that at least 5 of the first 10 sites contain the given keyword. (b) Compute the probability that the search engine had to visit at least 5 sites in order to find the first occurrence of a keyword.

Answer 1

(a) The probability that at least 5 of the first 10 sites contain the given keyword is 0.0328.

(b) The probability that the search engine had to visit at least 5 sites in order to find the first occurrence of a keyword is 0.4096.

Explanation:

(a)

Let X = number of sites that contains the keyword.

The probability that a site contains the keyword is, p = 0.20.

The number of sites visited first is n = 10.

The random variable X follows a Binomial distribution with parameter n and p.

The probability mass function of X is:

`P(X=x)={10\choose x}0.20^(x)(1-0.20)^(10-x);\ x=0,1,2,3...`

Compute the probability that at least 5 of the first 10 sites contain the given keyword as follows:

P (X ≥ 5) = 1 - P (X < 5)

= 1 - P (X = 0) - P (X = 1) - P (X = 2) - P (X = 3) - P (X = 4)

`=1-\sum\limits^(4)_(x=0) {10\choose x}0.20^(x)(1-0.20)^(10-x)\\=1-0.1074-0.2684-0.3020-0.2013-0.0881\\=0.0328`

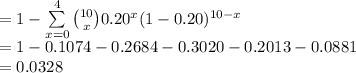
Thus, the probability that at least 5 of the first 10 sites contain the given keyword is 0.0328.

(b)

Let Y = number of sites that contains the keyword.

The probability that a site contains the keyword is, p = 0.20.

The random variable Y follows a Geometric distribution with parameter p.

The probability mass function of Y is:

`P(Y=y)=(1-p)^(x-1)p;\ x=1,2,3...`

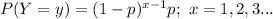
Compute the probability that the search engine had to visit at least 5 sites in order to find the first occurrence of a keyword as follows:

P (X ≥ 5) = 1 - P (X ≤ 4)

`=1-\sum\limits^(4)_(x=1) (1-0.20)^(x-1)0.20\\=1-0.20-0.16-0.128-0.1024\\=0.4096`

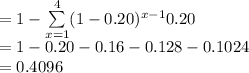
Thus, the probability that the search engine had to visit at least 5 sites in order to find the first occurrence of a keyword is 0.4096.