Question

The standard test to determine the maximum lateral acceleration of a car is to drive it around a 200-ft-diameter circle painted on a level asphalt surface. The driver slowly increases the vehicle speed until he is no longer able to keep both wheel pairs straddling the line. A 3000 lb car is traveling at 25 mi/hr when the driver applies the brakes, and the car continues to move along the circular path. What is the maximum deceleration possible if the tires are limited to a total horizontal friction force of 2400 lb?

Answer 1

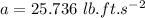`a=25.736\ lb.ft.s^(-2)` is the maximum deceleration from this top speed keeping-up with the grip of friction.

Step-by-step explanation:

Given:

diameter of the track,
`d=200\ ft`

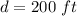
mass of the car,
`m=3000\ lb`

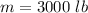
speed of the car,
`v=25\ mi.hr^(-1)=36.6667\ ft.s^(-1)`

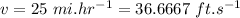
maximum horizontal frictional force between the surfaces,
`f=2400* 32.17=77208\ lb.ft.s^(-2)`

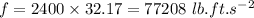
Now the maximum speed attained by the car according to the frictional force:

`f=m.(v^2)/(r)` also
`f=m.a`

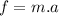
where:

• a = acceleration;
  `(v^2)/(r) =a`

• 
  `r=(d)/(2) =100\ ft`

`77208=3000* (v^2)/(r)`

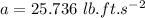`a=25.736\ lb.ft.s^(-2)` is the maximum deceleration from this top speed keeping-up with the grip of friction.