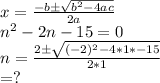Answer:
Explanation:
1. by making factors
consider ax²+bx+c=0
if a×c or ac>0 , then break b=d+e such that de=ac
if ac<0,then write b=d-e (e.g.,5-2=3)
such that de=ac
here n²-2n-15
1×-15=-15
-2=-(5-3)
5×-3=-15
n²-2n-15=n²-(5-3)n-15
=n²-5n+3n-15
=n(n-5)+3(n-5)
=(n-5)(n+3)
roots are n-5=0,n=5 and n+3=0,n=-3
2. by using formula
ax²+bx+c=0