Question

A certain car averages 27.1 mpg with a standard deviation of 1.4 MPG if miles per gallon is normally distributed what is the minimum miles per gallon that puts a car in the top 30% of gas mileage

Answer 1

27.83 mpg is the minimum miles per gallon that puts a car in the top 30% of gas mileage.

Explanation:

We are given the following information in the question:

Mean, μ = 27.1 mpg

Standard Deviation, σ = 1.4

We are given that the distribution of miles per gallon is a bell shaped distribution that is a normal distribution.

Formula:

`z_(score) = \displaystyle(x-\mu)/(\sigma)`

We have to find the value of x such that the probability is 0.3

`P( X > x) = P( z > \displaystyle(x - 27.1)/(1.4))=0.3`

`= 1 -P( z \leq \displaystyle(x - 27.1)/(1.4))=0.3`

`=P( z \leq \displaystyle(x - 27.1)/(1.4))=0.7`

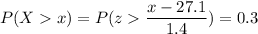
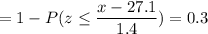
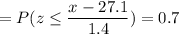
Calculation the value from standard normal z table, we have,

`\displaystyle(x - 27.1)/(1.4) = 0.524\\\\x = 27.83`

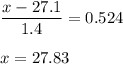
Thus, 27.83 mpg is the minimum miles per gallon that puts a car in the top 30% of gas mileage.