Answer:
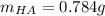
Step-by-step explanation:
Hello,
In this case, considering the dissociation of thiamine hydrochloride:
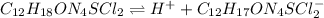
It is convenient to write it as:
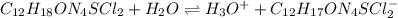
Or:

With which the Henderson-Hasselbalch equation is applied:
![pH=pKa+log(([A^-])/([HA]) )](https://img.qammunity.org/2021/formulas/chemistry/college/4jekuzp3zwdrzip42pcpqbrue6e3ty3yh6.png)
Therefore:
![log(([A^-])/([HA]) )=3.50-[-log(3.37x 10^(-7))]=3.50-6.47=-2.97}\\\\([A^-])/([HA]) =10^(-2.97)=1.07x10^(-3)](https://img.qammunity.org/2021/formulas/chemistry/college/7hnn2o2gw8nn6ta1dona5c1x1n92xsvd8f.png)
![[A^-]=1.07x10^(-3)}[HA]](https://img.qammunity.org/2021/formulas/chemistry/college/e28lj3bpyx847y0d0whfs0jxv7z9ntyx8s.png)
Thus, as the pH equals the concentration of hydrogen which also equals the concentration of the conjugate base, one obtains:
![[H]^+=[A^-]=10^(-pH)=10^(-3.50)=3.16x10^(-4)M](https://img.qammunity.org/2021/formulas/chemistry/college/o7wps5jgz036rdn6euvw6j1q4soqv2jtn4.png)
Now, solving for the concentration of acid ([HA]):
![[HA]=(3.16x10^(-4)M)/(1.07x10^(-3)) =0.296M](https://img.qammunity.org/2021/formulas/chemistry/college/ifx9s7qfuuhm5f5lfnc1pscpbva82fu5vc.png)
Finally, the mass turns out:
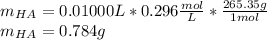
Best regards.