Question

Thiamine hydrochloride (C12H18ON4SCl2) is a water-soluble form of thiamine (vitamin B1; Ka = 3.37×10−7). How many grams of the hydrochloride must be dissolved in 10.00 mL of water to give a pH of 3.50?

Answer 1

`m_(HA)=0.784g`

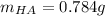
Step-by-step explanation:

Hello,

In this case, considering the dissociation of thiamine hydrochloride:

`C_(12)H_(18)ON_4SCl_2 \rightleftharpoons H^++C_(12)H_(17)ON_4SCl_2^-`

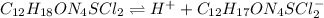
It is convenient to write it as:
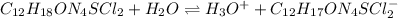
`C_(12)H_(18)ON_4SCl_2+H_2O \rightleftharpoons H_3O^++C_(12)H_(17)ON_4SCl_2^-`

Or:

`HA+H_2O\rightleftharpoons H_3O^++A^-`

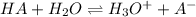
With which the Henderson-Hasselbalch equation is applied:

`pH=pKa+log(([A^-])/([HA]) )`

Therefore:

`log(([A^-])/([HA]) )=3.50-[-log(3.37x 10^(-7))]=3.50-6.47=-2.97}\\\\([A^-])/([HA]) =10^(-2.97)=1.07x10^(-3)`

`[A^-]=1.07x10^(-3)}[HA]`

Thus, as the pH equals the concentration of hydrogen which also equals the concentration of the conjugate base, one obtains:

`[H]^+=[A^-]=10^(-pH)=10^(-3.50)=3.16x10^(-4)M`

Now, solving for the concentration of acid ([HA]):

`[HA]=(3.16x10^(-4)M)/(1.07x10^(-3)) =0.296M`

Finally, the mass turns out:

`m_(HA)=0.01000L*0.296(mol)/(L)*(265.35g)/(1mol)\\ m_(HA)=0.784g`

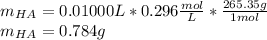
Best regards.