Question

Assuming the volume of a trigonal prism, who has a side of 10cm and a length of 20 cm, is 866cm^3, what is its surface area?

Answer 1

The surface area of the triangular prism is 686.6 cm².

Explanation:

Step 1:

The volume of a triangular prism can be determined by multiplying its area of the triangular base with the length of the prism.

The base triangle has a base length of 10 cm and assume it has a height of h m.

The volume of the prism
`= (1)/(2) (b)(h) (length) = (1)/(2) (10)(h)(20) = 866.`

`h = (866(2))/(10(20)) = 8.66.`

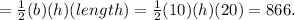
The height of the triangle is 8.66 cm.

Step 2:

The surface area of the triangle is obtained by adding all the areas of the shapes in the prism. There are 2 triangles and 3 rectangles in a triangular prism.

The triangles have a base length of 10 cm and a height of 8.66 cm. A triangles area is half the product of its base length and height.

The rectangles all have a length of 20 cm and a width of 10 cm. The area of a rectangle is the product of its length and width.

The area of the 2 triangles
`= 2 [(1)/(2) (10)(8.66)] = 86.6.`

The area of the 3 rectangle
`= 3[(20)(10)] = 600.`

Step 3:

The surface area of the triangular prism
`= 86.6 + 600 = 686.6.`

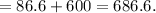
The surface area of the prism is 686.6 cm².