Answer:
a) τ = i ^ (y
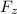 - z
- z
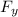 ) + j ^ (z Fₓ - x
) + j ^ (z Fₓ - x
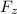 ) + k ^ (x
) + k ^ (x
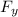 - y Fₓ)
- y Fₓ)
b)τ = (-0.189i ^ -5.6 j ^ + 33.978k ^) N m
c)α = (-7.8 10⁻⁴ i ^ - 2.3 10⁻² j ^ + 1.4 10⁻¹ k ^) rad / s²
Step-by-step explanation:
a) Torque is given by
τ = r x F
The easiest way to solve this equation is in the form of a determinant
![\tau =\left[\begin{array}{ccc}i&j&k\\x&y&z\\F_(x)&F_(y) &F_(z)\end{array}\right]](https://img.qammunity.org/2021/formulas/physics/college/k8r15h2pjrp8cfq3i16t0eg36c73ucknco.png)
The result is
τ = i ^ (y
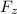 - z
- z
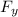 ) + j ^ (z Fₓ - x
) + j ^ (z Fₓ - x
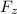 ) + k ^ (x
) + k ^ (x
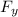 - y Fₓ)
- y Fₓ)
b) let's calculate
τ = i ^ (0.075 1.4 -0.035 8.4) + j ^ (0.035 2.8 - 4.07 1.4) + k ^ (4.07 8.4 - 0.075 2.8)
τ = i ^ (- 0.189) + j ^ (-5.6) + k ^ (33,978)
τ = (-0.189i ^ -5.6 j ^ + 33.978k ^) N m
c) calculate the angular acceleration with
τ = I α
α = τ / I
Since the moment of inertia is a scalar, the direction does not change, only the modulus of each element changes.
α = (-0.189i^ -5.6 j^ + 33.978k^) / 241
α = (-7.8 10⁻⁴ i ^ - 2.3 10⁻² j ^ + 1.4 10⁻¹ k ^) rad / s²