Answer:
An equation of the new function in vertex form is
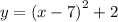 .
.
Explanation:
Consider parent function as
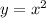 .
.
According to the transformation of graph,
The function
 shifts the function to right side by b units.
shifts the function to right side by b units.
So in this case, graph is translated to the right side by 7 units, so the parent function
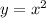 can be written as
can be written as
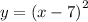
The function
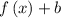 shifts the function in upward direction by b units.
shifts the function in upward direction by b units.
So in this case, graph is translated in upward by 2 units, so the function
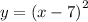 can be written as
can be written as
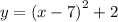
Now vertex form of quadratic equation is given as,
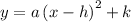
So the final equation is
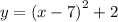 . .
. .