Question

URGENTLY NEED HELP WITH PHYSICS?

A vaulter is holding a horizontal 3.00-kg pole, 4.50 m long. His front arm lifts straight up on the pole, 0.750 from the end, and his back arm pushes straight down on the end of the pole. How much force does his back arm exert on the pole?

(Unit= N)

NEED HELP FAST

Answer 1

58.8 N

Step-by-step explanation:

Let 'F₁' be the force by front arm and 'F₂' be the force by back arm.

Given:

Mass of the rod (m) = 3.00 kg

Length of the pole (L) = 4.50 m

Acceleration due to gravity (g) = 9.8 m/s²

Distance of 'F₁' from one end of pole (d₁) = 0.750 m

'F₂' acts on the end. So, distance between 'F₁' and 'F₂' = 0.750 m

Now, weight of the pole acts at the center of pole.

Now, distance of center of pole from 'F₁' is given as:

d₂ = (L ÷ 2) - d₁

`d_2=(4.50)/(2)-0.75=1.5\ m`

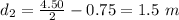
Now, as the pole is held horizontally straight, the moment about the point of application of force 'F₁' is zero for equilibrium of the pole.

So, Anticlockwise moment = clockwise moment

`F_2* d_1=mg* d_2\\\\F_2=(mg* d_2)/(d_1)`

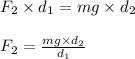
Plug in the given values and solve for 'F₂'. This gives,

`F_2=(3.00\ kg* 9.8\ m/s^2* 1.5\ m)/(0.75\ m)\\\\F_2=(44.1)/(0.75)=58.8\ N`

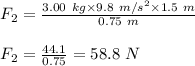
Therefore, the force exerted by the back arm on the pole is 58.8 N vertically down.