Answer:

Explanation:
Given Two points are :
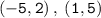
To Find:
The Slope
Solution:
We know that the formula of Slope is,
Note: Slope can be denoted as m.
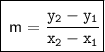
Here,
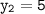
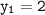
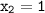
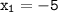
So put their values accordingly:
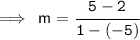
Now Simplify it.
Firstly, Simplify The numerator:
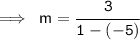
Now, Simplify The denominator:
- We know that (-) and (-) equals to (+).So,
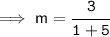
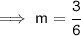
Use cancellation method and cancel 3 and 6 by 3:
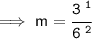
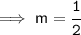
Hence, the slope of Two given points would be,
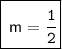

I hope this helps!