Answer:
Explanation:
Given that the volume V of a right circular cylinder of radius r and height h is
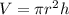
To find rate of change of V with respect to rate of change of radius
Here given that h is constant
So differentiation with respect to t gives
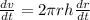
This would be dv/dt i.e. rate of change of volume with respect to time in terms of dr/dt
This varies whenever r varies