Question

A publisher reports that 79% of their readers own a personal computer. A marketing executive wants to test the claim that the percentage is actually more than the reported percentage. A random sample of 100 found that 89% of the readers owned a personal computer. Is there sufficient evidence at the 0.02 level to support the executive's claim

Answer 1

Yes, we have sufficient evidence at the 0.02 level to support the executive's claim.

Explanation:

We are given that a publisher reports that 79% of their readers own a personal computer. A marketing executive wants to test the claim that the percentage is actually more than the reported percentage. A random sample of 100 found that 89% of the readers owned a personal computer.

Let Null Hypothesis,
`H_0` : p
`\leq` 0.79 {means that the percentage is actually less than or equal to the reported percentage}

Alternate Hypothesis,
`H_1` : p > 0.79 {means that the percentage is actually more than the reported percentage}

The test statics that will be used here is One-sample proportions test;

T.S. =
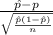`\frac{\hat p -p}{\sqrt{(\hat p(1-\hat p))/(n) } }` ~ N(0,1)

where,
`\hat p` = % of the readers who owned a personal computer in a sample of 100 = 89%

n = sample size = 100

So, test statistics =
`\frac{0.89 -0.79}{\sqrt{(0.89(1-0.89))/(100) } }`

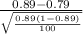
= 3.196

Now, at 0.02 level of significance the z table gives critical value of 2.054. Since our test statistics is more than the critical value of z so we have sufficient evidence to reject null hypothesis as it fall in the rejection region.

Therefore, we conclude that percentage is actually more than the reported percentage which means we have sufficient evidence at the 0.02 level to support the executive's claim.