Question

I need help solving this question with explaining please
ANSWER ASAP!!!!!!!!!

Answer 1

x = 85 degrees and

y = 45 degrees.

Explanation:

Step 1:

The angle for a straight line is 180°. The sum of the angles in a triangle is 180°. These two statements are required to solve this problem.

The angles of x° and 95° are on a single straight line.

So
`x^(\circ) + 95^(\circ) = 180^(\circ).`

`x^(\circ) = 180^(\circ) - 95^(\circ) = 85^(\circ) .`

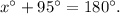
So the angle of x is 85°.

Step 2:

The sum of the angles in a triangle is 180°.

So
`50^(\circ) + x^(\circ) + y^(\circ) =180^(\circ).`

`50^(\circ) + 85^(\circ) + y^(\circ) =180^(\circ).`

`y^(\circ) =180^(\circ) - 135^(\circ), y = 45 ^(\circ).`

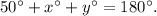
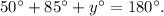
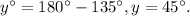
So the angle of y is 45°.