Answer:
(1.5,-2.6)
Explanation:
Given the polar coordinates (-3,60°).
Let our Cartesian coordinates be (x,y)
#We know that when converting the rectangular coordinates (x,y) to polar (r,θ), then:
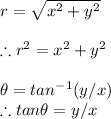
#Using the illustration above, we can express our polar coordinates as:
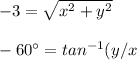
#Solve simultaneously to solve for x and y:
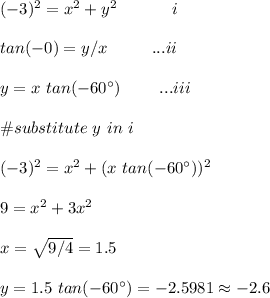
Hence, the Cartesian coordinates are (1.5,-2.6)