Question

Consider a system made of a ramp that has a run of 8 m and a rise of 6 m. Two equal masses of 4-kg are connected to each other by a massless string pulled tight across a massless pulley: one block rests on the slope of the ramp and the other block hangs from the pulley without moving or touching anything. The system, therefore, is at rest. What is the force of friction (in N) acting on the block resting on the ramp

Answer 1

The force of friction is 15.68 N.

Step-by-step explanation:

Given:

Rise is 6 m and run is 8 m.

Mass of each body (m) = 4 kg

The whole system is in equilibrium.

Now, consider the diagram below representing the scenario given in the question.

The forces acting on the mass that is hanging are tension force in the upward direction and weight of the body acting vertically downward.

As the mass is in equilibrium, the total upward force equals total downward force. So,

`T= mg=4* 9.8=39.2\ N` -------- (1)

Now, the forces acting on the other mass along the ramp are:

1. Tension (T) up the ramp

2.
`mg sin\theta` and frictional force (f) down the ramp

Now, as per question:

Rise = 6 m and run = 8 m

So, from figure,

`\tan\theta=(6)/(8)=0.75\\\\\theta=\tan^(-1)(0.75)=37\°`

Now,
`\sin\theta=\sin(37\°)=0.6`

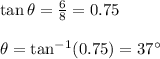
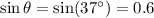
Now, as the other mass is also at rest, net force acting on it is also 0. So,

`F_(net)=0\\\\T-(mg\sin\theta+f)=0\\\\mg\sin\theta+f=T\\\\f=T-mg\sin\theta`

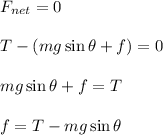
Now, plug in the given values and solve for 'f'. This gives,

`f=39.2-(4* 9.8* 0.6)\\\\f=39.2-23.52=15.68\ N`

Therefore, the force of friction is 15.68 N