Question

Type A is 5 feet tall and grows at a rate of 9 inches per year. Type B is 8 feet tall and grows at a rate of 6 inches per year. Algebraically determine exactly how many years it will take for these trees to be the same height.

Answer 1

After 12 years height of both the trees would be same.

Explanation:

Given,

Height of tree type A = 5 ft

Height of tree type B = 8 ft

We need to find after how many years both the trees will be of same height.

Solution,

Firstly we will convert the height of both plants into inches.

Since we know that 1 feet is equal to 12 inches.

So height of tree type A =
`5\ ft=5*12=60\ in`

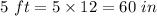
Similarly, height of tree type B =
`8\ ft=8*12=96\ in`

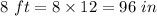
Also given that;

Rate of growth of tree type A = 9 in/year

and rate of growth of tree type A = 6 in/year

Let the number of years be 'x'.

So according to question after 'x' years the height of both trees type A and type B will be same.

Now we can frame the equation as;

`60+9x=96+6x`

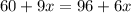
Combining the like terms, we get;

`9x-6x=96-60\\\\3x=36`

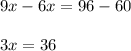
On dividing both side by '3' using division property, we get;

`(3x)/(3)=(36)/(3)\\\\x=12`

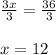
Hence after 12 years height of both the trees would be same.