Answer:
The answer to your question is Yes, the point P lies on the circle
Explanation:
Data
P (2
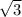 , 2)
, 2)
Center (0, 0)
Q (0, -4)
Process
1.- Find the radius of the circle
dCQ =
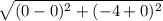
dCQ =
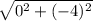
dCQ =
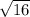
dCQ = 4
2.- Find the equation of the circle
(x - 0)² + (y - 0)² = 4²
-Simplification
x² + y² = 16
3.- Substitute P in the equation of the circle
(2
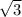 )² + (2)² = 16
)² + (2)² = 16
4(3) + 4 = 16
12 + 4 = 16
16 = 16
4.- Conclusion
The point (2
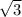 , 2) lies on the circle because when we evaluate the equation of the circle with this point, we get the length of the radius.
, 2) lies on the circle because when we evaluate the equation of the circle with this point, we get the length of the radius.