Question

A (20*20) cm² loop has a resistance of 0.10 Ω. A magnetic field perpendicular to the loop is B = 4t - 2t², where B is in tesla and t is in seconds.

What is the current in the loop at t = 0.0 s, t = 1.0 s, and t = 2.0 s?

Answer 1

Step-by-step explanation:

Area, A = 20 x 20 cm² = 0.04 m²

Resistance, R = 0.10 ohm

Magnetic field, B = 4t - 2t²

the induced emf is given by

`e=(d\phi )/(dt)`

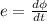
where, Ф i the flux linked with the coil.

`e=A* (dB )/(dt)`

`e=0.04(4 - 4t)`

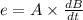
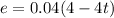
Induced current

i = e/ R

`i=(0.04(4 - 4t))/(0.1)`

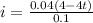
i = 0.4(4 - 4t)

For t = 0 s

i = 0.4 x 4 = 1.6 A

For t = 1 s

i = 0.4 ( 4 - 4) = 0 A

For t = 2 s

i = 0.4 ( 4 - 8) = 1.6 A in opposite direction

Answer 2

Answer with Explanation:

We are given that

Area of loop=
`(20* 20) cm^2=400* 10^(-4) m^2`

`1 cm^2=10^(-4) m^2`

Resistance, R=
`0.1\Omega`

B=
`4t-2t^2`

We know that magnetic flux

`\phi=BA`

Emf ,
`E=\mid (d\phi)/(dt)\mid =\mid(d(BA)/(dt)\mid =\mid A(dB)/(dt)=400* 10^(-4)* (4t-2t^2)/(dt)\mid =\mid400* 10^(-4)*(4-4t)\mid`

Current,
`I=(E)/(R)`

Current,
`I=(\mid 400* 10^(-4)(4-4t)\mid )/(0.1)=1.6\mid (1-t)\mid`

Substitute t=0 s

Then, I=
`1.6\mid (1-0)\mid`=1.6 A

Substitute t=1 s

Then, I=
`1.6\mid (1-1)\mid`=0

Substitute

t=2 s

Current, I=
`1.6\mid(1-2)\mid`=1.6 A