Question

In the third week of July, a random sample of 40 farming regions gave a sample mean of x = $6.88 per 100 pounds of watermelon. Assume that σ is known to be $1.98 per 100 pounds.

A farm brings 15 tons of watermelon to the market.
Find a 90% confidence interval for the population mean cash value of this crop. What is the margin of error? Hint: 1 ton is 2000 pounds. (Round your answers to two decimal places.)

Answer 1

a. [6.6350,7.3950]

b. ME=0.5150

Explanation:

a. Given that n=40,
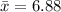`\bar x=6.88` and that:
`z_(\alpha/2)=z_(0.05)=1.645`

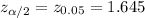
The required 90% confidence interval can be calculated as:

`\bar x\pm(margin \ of \ error)\\\\\bar x\pm z_(\alpha/2)(\sigma)/(√(n))\\\\6.88\pm(1.645* (1.98)/(√(40)))\\\\=[6.3650,7.3950]`

Hence, the 90% confidence interval for the population mean cash value of this crop is [6.6350,7.3950]

b. The margin of error at 90% confidence interval is calculated as:

`ME= z_(\alpha/2)(\sigma)/(√(n))\\\\=(1.645* (1.98)/(√(40)))\\\\=0.5150`

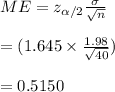
Hence, the margin of error is 0.5150