Question

In an out of control ceramics workshop, two clay balls collide in mid air and stick together. The first has mass 3.12 kg and collides with a second that is initially at rest. The composite system moves with a speed equal to one-third the original speed of the 3.12 kg ball. What is the mass of the second sphere

Answer 1

The mass of the second sphere is 6.24 kg.

Step-by-step explanation:

Let the mass of second sphere be 'm₂' kg.

Given:

Mass of first sphere (m₁) = 3.12 kg

Initial speed of first sphere = 'u₁' (Assume)

Initial speed of second sphere (u₂) = 0 m/s

Final speed of system is one-third of 'u₁'. Let 'v' be the final speed.

So,
`v=(u_1)/(3)`

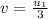
Now, the conservation of momentum holds true for the collision system.

Initial momentum is given as:

`P_i=m_1u_1+m_2u_2=m_1u_1+0=m_1u_1`

Final momentum is given as:

`P_f=(m_1+m_2)v=(u_1)/(3)(m_1+m_2)`

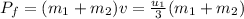
Now, from conservation of momentum, we have:

`P_i=P_f\\\\m_1u_1=(u_1)/(3)(m_1+m_2)\\\\3m_1=m_1+m_2\\\\m_2=3m_1-m_1=2m_1`

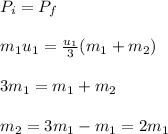
Plug in 3.12 kg for m₁ and solve for
`m_2`. This gives,

`m_2=2* 3.12\ kg = 6.24\ kg`

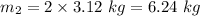
Therefore, the mass of the second sphere is 6.24 kg.