Answer:
The value of total entropy change during the process
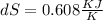
Step-by-step explanation:
mass of iron
 = 25 kg
= 25 kg
Initial temperature of iron
 = 350°c = 623 K
= 350°c = 623 K
Mass of water
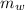 = 100 kg
= 100 kg
Initial temperature of water
 = 180°c = 453 K
= 180°c = 453 K
When iron block is quenched inside the water the final temperature of both iron & water becomes equal. this is =

Thus heat lost by the iron block = heat gain by the water
⇒

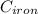 (
(
 -
-
 ) =
) =
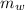
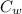 (
(
 -
-
 )
)
⇒ 25 × 0.448 × (
 -
-
 ) = 100 × 4.2 × (
) = 100 × 4.2 × (
 -
-
 )
)
⇒
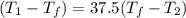
⇒
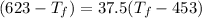
⇒

⇒
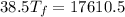
⇒
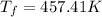
This is the final temperature after quenching.
The total entropy change is given by,
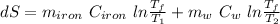
Put all the values in above formula,
 25 × 0.448 ×
25 × 0.448 ×
 + 100 × 4.2 ×
+ 100 × 4.2 ×
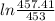
 - 3.46 + 4.06
- 3.46 + 4.06
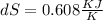
This is the value of total entropy change.