Answer:
The given system of equations
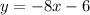 and
and
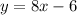 has exactly one solution
has exactly one solution
Explanation:
Given that the system of equations
 and
and
 has exactly one solution
has exactly one solution
For :
Now to show that the given system of equations has exactly one solution :
Solving the given equations (1) and (2) to get solution
Adding the equations (1) and (2) we get
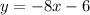
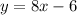
______________
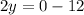
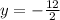

Therefore the value of is y=-6
Substitute the value of y in equation (1) we have
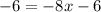
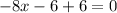
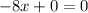
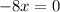
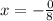

Therefore the value of x is x=0
Therefore it has exactly one solution is (0,-6)
Therefore the given system of equations
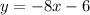 and
and
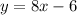 has exactly one solutione given system of equations has exactly one solution
has exactly one solutione given system of equations has exactly one solution