Answer: The potential of the given cell is 1.551 V
Step-by-step explanation:
The given chemical cell follows:
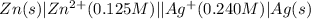
Oxidation half reaction:
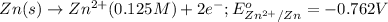
Reduction half reaction:
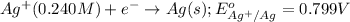 ( × 2)
( × 2)
Net cell reaction:
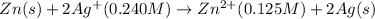
Oxidation reaction occurs at anode and reduction reaction occurs at cathode.
To calculate the
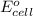 of the reaction, we use the equation:
of the reaction, we use the equation:
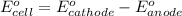
Putting values in above equation, we get:

To calculate the EMF of the cell, we use the Nernst equation, which is:
![E_(cell)=E^o_(cell)-(0.059)/(n)\log ([Zn^(2+)])/([Ag^(+)]^2)](https://img.qammunity.org/2021/formulas/chemistry/college/bpvmmer1tv4ns0biwe1gmtmn21escj01p0.png)
where,
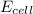 = electrode potential of the cell = ? V
= electrode potential of the cell = ? V
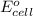 = standard electrode potential of the cell = +1.561 V
= standard electrode potential of the cell = +1.561 V
n = number of electrons exchanged = 2
![[Zn^(2+)]=0.125M](https://img.qammunity.org/2021/formulas/chemistry/college/q49h74eg8j5xm3kaoh9f71bb2xoe5v08fx.png)
![[Ag^(+)]=0.240M](https://img.qammunity.org/2021/formulas/chemistry/college/frc4orv95phnhh36ovu6t8bs7tppzkdkmx.png)
Putting values in above equation, we get:
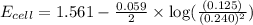
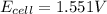
Hence, the potential of the given cell is 1.551 V