Answer:
230.38 mm
Explanation:
The distance traveled by the tip of the hands is (part of) the circumference of the circle with radius of the lengths of the hands.
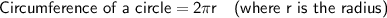
Radii
Larger circle (minute hand):
- r = 200% of 20 mm = 40 mm
Smaller circle (hour hand):
Minute Hand
The minute hand does a full rotation of the circle in one hour.
Therefore, the distance it travels in one hour is the complete circumference of a circle with radius 40 mm:

Hour Hand
There are 12 numbers on a clock.
The hour hand travels from one number to the next in one hour.
Therefore, the distance it travels in one hour is 1/12th of the circumference of the circle:

To find how much farther the tip of the minute hand moves than the tip of the hour hand, subtract the latter from the former:
