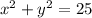Question

Write the equation in standard form for the circle that has a diameter with endpoints (5,0) and (–5,0).

Answer 1

The equation of the circle is
`x^2+y^2=25`

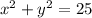
Step-by-step explanation:

Given that the endpoints of the circle.

The coordinates of the endpoints are (5,0) and (-5,0)

Center:

The center of the circle can be determined using the midpoint formula,

`Center=((x_1+x_2)/(2),(y_1+y_2)/(2))`

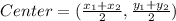
Substituting the diameters of the circle (5,0) and (-5,0), we get,

`Center=((5-5)/(2),(0-0)/(2))`

`Center=(0,0)`

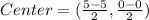
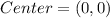
Thus, the coordinates of the center is (0,0)

Radius:

The radius of the circle can be determined using the distance formula,

`r=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2`

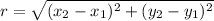
Substituting the center (0,0) and one of the endpoints (5,0), we get,

`r=\sqrt{(5-0)^2+(0-0)^2`

`r=\sqrt{(5)^2+(0)^2`

`r=√(25)`

`r=5`

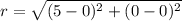
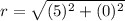
Thus, the radius of the circle is 5 units.

Equation of the circle:

The equation of the circle can be determined using the formula,

`(x-h)^(2)+(y-k)^(2)=r^(2)`

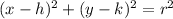
where center = (h,k) = (0,0) and r = 5 units

Substituting, we get,

`(x-0)^2+(y-0)^2=5^2`

`x^2+y^2=25`

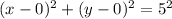
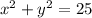
Thus, the equation of the circle in standard form is
`x^2+y^2=25`