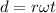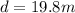Question

A disk 7.98 cm in radius rotates at a constant rate of 1 250 rev/min about its central axis. (a) Determine its angular speed. rad/s (b) Determine the tangential speed at a point 3.10 cm from its center. m/s (c) Determine the radial acceleration of a point on the rim. magnitude km/s2 direction (d) Determine the total distance a point on the rim moves in 1.90 s. m

Answer 1

Answer with Explanation:

We are given that

Radius of disk=r=7.98 cm=0.0798 m

1 m=100 cm

a.Angular speed=1250rev/min

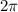`2\pi` rad=1 rev

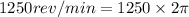`1250 rev/min=1250* 2\pi` rad/min

1 min=60 sec

Angular speed=
`\omega=(1250* 2\pi)/(60) rad/s`

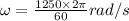
Angular speed=
`\omega=130.9 rad/sec`

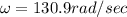
b.r=3.1 cm=
`(3.1)/(100)=0.031m`

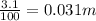
1 m=100 cm

`v=r\omega=0.031* 130.9=4.058m/s`

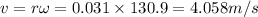
Hence, the tangential speed=4.058m/s

c.Radial acceleration=
`a=r\omega^2=(130.9)^2(0.0798)=1367.36m/s^2`

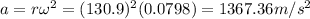
Hence, the radial acceleration of a point on the rim=
`1367.36 m/s^2`

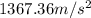
d.Time, t=1.9 s

Total distance=
`d=r\omega t`

`d=0.0798* 130.9* 1.9`

`d=19.8 m`